How To Find Fixed Points Of A System Of Differential Equations
Fixed Points And Stability Of A Nonlinear System Youtube
How to find fixed points of a system of differential equations. An example is shown in the first. For the next iteration we get. The Jacobian of the differential equations is J 2aαb αa 2a αb β αa 1 β.
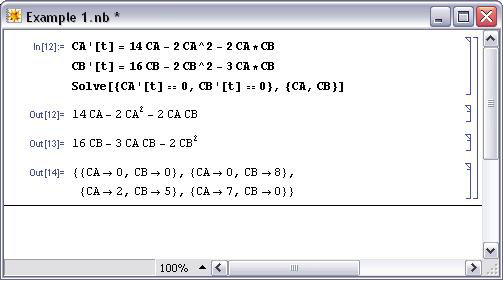
We can immediately deduce that at steady state T_n - ab. We can use Mathematica to solve for the fixed point of this system and check our results. Choose initial conditions x0.
Browse other questions tagged differential-equations numerical-integration nonlinear or ask your own question. In these circumstances all orbits spiral outward and the fixed point is an unstable spiral. Alternatively you could use the differential equations to.
A different rearrangement for the equations has the form. Ode45 to do the integration. Stability of a fixed point can be determined by eigen values of matrix.
It can be understood as an. A b αβa0 1β1α. The Jacobian evaluated at the first equilibrium point is J αb 0 αb β 1 β.
Using an initial guess of and yields the following. You can also use all the tricks of. The nature of the fixed point depends on the eigenvalues of the stability matrix which are.
Developing an effective predator-prey system of differential equations is not the subject of this chapter. In summary our system of differential equations has three critical points 00 01 and 32.
Equilibrium Points For Nonlinear Differential Equations Youtube
Formal Computational Skills Ppt Video Online Download
Finding Fixed Points In Discrete Time Models Part 1 Youtube
Find The Fixed Point Of The Differential Equations Chegg Com
Nonlinear Ode Fixed Points And Linear Stability Youtube
Solved 5 Consider The Autonomous Nonlinear System Of Chegg Com
Fixed Point Of A 2x2 Linear System Of Odes Wolfram Demonstrations Project
10 1 Finding Fixed Points In Odes And Boolean Models Engineering Libretexts
Dynamical Systems 3 Nonlinear Systems Ing Jaroslav Jra
Stability Of A Fixed Point In A System Of Ode Application Center
Stablility Of Fixed Point Of A Dynamical System Aditya M Deshpande
Dynamical Systems 3 Nonlinear Systems Ppt Video Online Download
Find Fixed Points For A System Of Non Linear Differential Equations Mathematics Stack Exchange
Type Of Fixed Point Of A Autonomous Homogeneous Ordinary Differential Equation How To Solve Mathematical Problems Is A Challenge For Us
Equilibrium Point Wikipedia
Fixed Point Of A 2x2 Linear System Of Odes Wolfram Demonstrations Project
Dynamical Systems 3 Nonlinear Systems Ing Jaroslav Jra
Equilibrium Points Of Linear Autonomous Systems
Solved 2 A Model Of Two Populations Consider A Model For Two Chegg Com
Consider The System Of Differential Equations 1 Find The Fixed Points Of The System 2 Eval Homeworklib
Fixed Point Mathematics Wikipedia
Nonlinear Delay Differential Equations And Their Application To Modeling Biological Network Motifs Nature Communications
Fixed Point Theory Approach To Existence Of Solutions With Differential Equations Intechopen
Equilibrium Point Formula
Fixed Point Theory And Algorithms For Sciences And Engineering Home Page
Ode S Mathgrapher
Multiple Fixed Point Theorems And Applications In The Theory Of Odes
Bifurcation Points Of Differential Equation Example Mathematics Stack Exchange
Core Ac Uk
Pdf Fixed Points And Problems In Stability Theory
Solved Consider The Differential Equation System I T2 2x Y J I 3y Sketch The Nullclines And Find All Fixed Points B Classify The Fixed Points Of The System
Dynamical Systems 3 Nonlinear Systems Ppt Video Online Download
A K Dimensional System Of Fractional Neutral Functional Differential Equations With Bounded Delay Topic Of Research Paper In Mathematics Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science
Alun Math Ncsu Edu
Qualitative Analysis For Second Order Ode
Benchmarking Of Numerical Integration Methods For Ode Models Of Biological Systems Scientific Reports
Staff Science Uu Nl
Formal Computational Skills Dynamical Systems Analysis Dynamical Systems
Pdf Note On The Stability For Linear Systems Of Differential Equations
Differential And Integral Calculus An Introductory Course For Colleges And Engineering Schools He Equation Of The System Of Normals To Any Curve Is Ss X Xi Y
Fixed Point From Wolfram Mathworld
Ordinary Differential Equations Final Humanvszombies
Math Uchicago Edu
The Stability Of Equilibria Of A Differential Equation Math Insight
On Applications Of Coupled Fixed Point Theorem In Hybrid Differential Equations Of Arbitrary Order Zibeline International Publishing
10 1 Finding Fixed Points In Odes And Boolean Models Engineering Libretexts
Team Sjtu Biox Shanghai Judge A System 2009 Igem Org
Nonlinear Dynamics I Chaos Fall 2012 2 050j 12 006j 18 353j
3
Alternatively you could use the differential equations to calculate the trajectory.
Ydotx and then express dotyddotx in terms of x and y and then find the. Browse other questions tagged differential-equations numerical-integration nonlinear or ask your own question. Alternatively you could use the differential equations to. Eigen values of are therfore. Unfortunately most problems that arise in the real world are not linear and in most cases nonlinear systems can not be solvedthere is typically no method. An example is shown in the first. First let us rewrite the system of differentials in matrix form. Gx y x. So gntl converges to some point say gtl E Y.
In mathematics the Banach fixed-point theorem also known as the contraction mapping theorem or contractive mapping theorem is an important tool in the theory of metric spaces. Numerical solutions of nonlinear systems of equations Tsung-Ming Huang Department of Mathematics National Taiwan Normal University Taiwan E-mail. Y0 and use eg. For the next iteration we get. However systems can arise from ntextth order linear differential equations as well. Choose initial conditions x0. Hence for each t E I gnt converges to an element say gt E Y ie g converges point-wise to the function g.
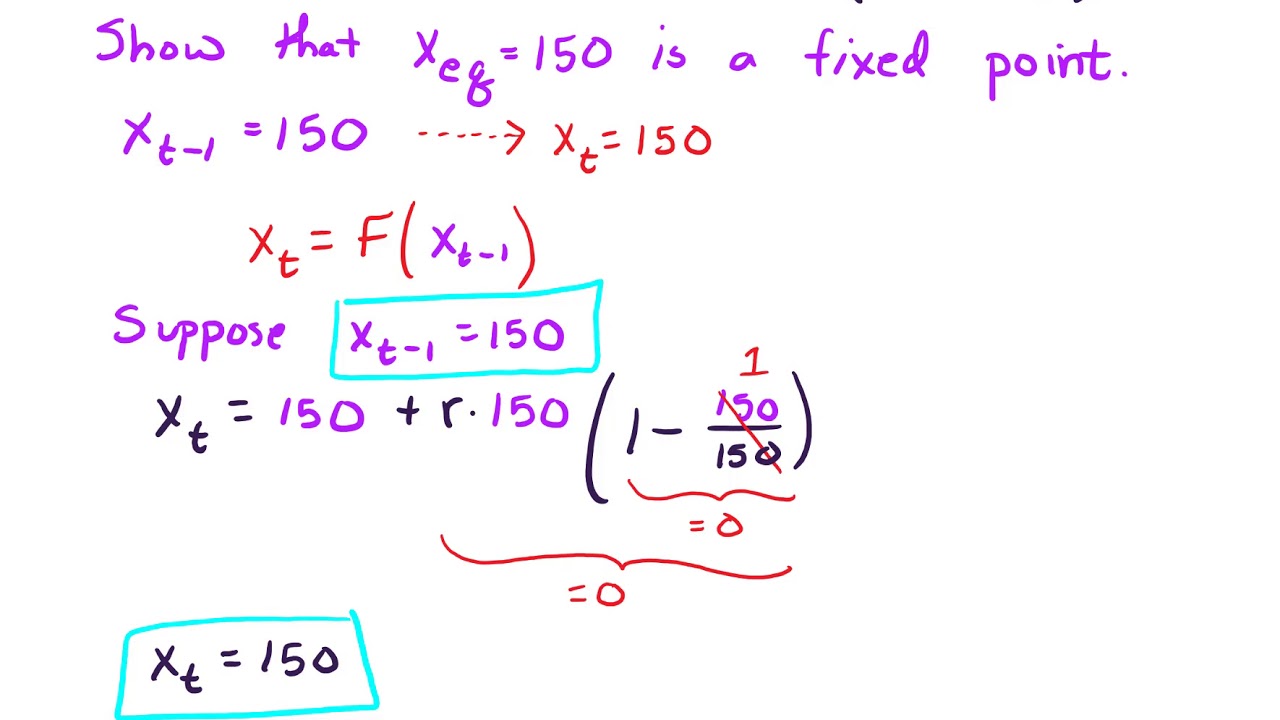
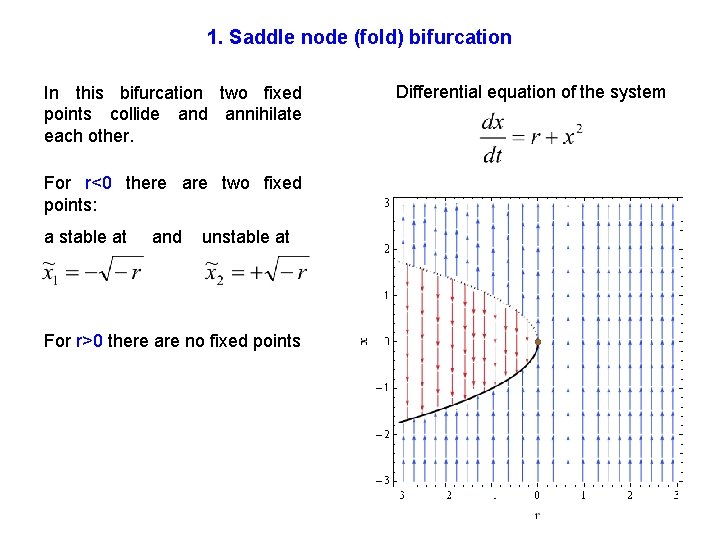
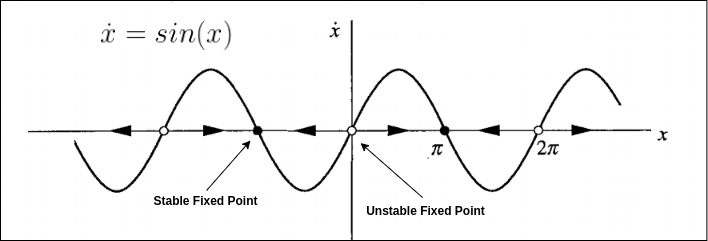
Post a Comment for "How To Find Fixed Points Of A System Of Differential Equations"